[BOJ] 2133번: 타일 채우기

https://www.acmicpc.net/problem/2133

2133번: 타일 채우기

문제

3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.

 

입력

첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.

 

출력

첫째 줄에 경우의 수를 출력한다.

 

---

풀이

📌 다이나믹 프로그래밍 (DP)

 

n이 1이라 하면 3x1 크기의 벽을 2x1, 1x2 크기의 타일로 채울 수 있는 경우는 없다.

n이 3일 때도 마찬가지로 한 칸이 비어 채울 수 없다.

따라서 홀수일 경우 타일로 채우는 경우의 수는 0이다.

 

n이 2일 때 아래 3가지 방법으로 채울 수 있다.

 

 

 

n이 4일 때 n이 2일 때의 타일을 조합하여 채울 수 있다.

하지만 아래의 2가지 경우는 n이 2일 때의 방법으로 구현할 수 없는 새로 추가된 케이스이다.

 

 

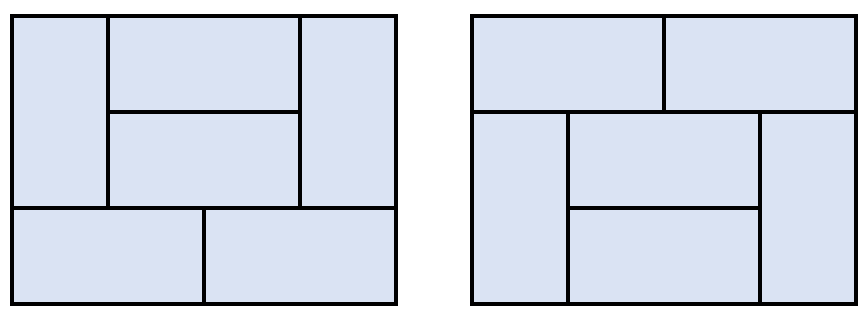
따라서 n=4일 때 경우의 수는 dp[4] = dp[2]*dp[2] + dp[2]*2 + 2이다.

 

 

n이 6일 때 n이 2일 때와 n이 4일 때의 타일을 조합하여 채울 수 있다.

ⅰ) n=4일 때와 n=2일 때의 조합

ⅱ) n=2일 때와 n=4일 때의 조합

 

하지만 ⅱ번의 경우는 ⅰ번과 중복되는 경우가 존재한다.

중복되는 경우를 제거하면 ⅱ번에서 n=4일 때의 조합을 n=2일 때의 방법으로 구현할 수 없는 케이스만을 다뤄야 한다.  => dp[4]*2 + dp[2]*2

 

또한 아래의 2가지 경우는 새로 추가된 케이스이다.

 

 

따라서 n=6일 때 경우의 수는 dp[6] = dp[4]*dp[2] + dp[2]*2 + 2이다.

 

이처럼 n이 짝수일 때 다음과 같은 점화식을 갖는다.

dp[n] = dp[n-2]*dp[2] + dp[n-4]*2 + dp[n-6]*2 +...

 

코드

#include <iostream>
using namespace std;

int main() {
  ios_base::sync_with_stdio(false);
  cin.tie(NULL);
  cout.tie(NULL);

  int n;
  cin >> n;

  if(n%2==1) {
    cout << 0;
    return 0;
  }
  
  int dp[31] = {0,};
  dp[0] = 1;
  dp[2] = 3;
  for(int i = 4; i <= n; i+=2) {
    for(int j = 0; j < i-2; j+=2) {
      dp[i] += dp[j]*2;
    }
    dp[i] += dp[i-2]*dp[2];
  }

  cout << dp[n];
  return 0;
}

 

결과